https://www.acmicpc.net/problem/9461
9461번: 파도반 수열
오른쪽 그림과 같이 삼각형이 나선 모양으로 놓여져 있다. 첫 삼각형은 정삼각형으로 변의 길이는 1이다. 그 다음에는 다음과 같은 과정으로 정삼각형을 계속 추가한다. 나선에서 가장 긴 변의
www.acmicpc.net
문제 설명
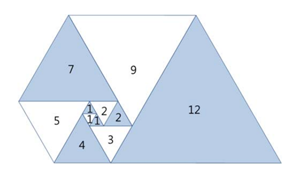
오른쪽 그림과 같이 삼각형이 나선 모양으로 놓여져 있다. 첫 삼각형은 정삼각형으로 변의 길이는 1이다. 그 다음에는 다음과 같은 과정으로 정삼각형을 계속 추가한다. 나선에서 가장 긴 변의 길이를 k라 했을 때, 그 변에 길이가 k인 정삼각형을 추가한다.
파도반 수열 P(N)은 나선에 있는 정삼각형의 변의 길이이다. P(1)부터 P(10)까지 첫 10개 숫자는 1, 1, 1, 2, 2, 3, 4, 5, 7, 9이다.
N이 주어졌을 때, P(N)을 구하는 프로그램을 작성하시오.

풀이 과정
- 나의 풀이
① 처음 문제를 마주쳤을 때 "나선 모양으로 특정 수들을 더하며 끊임없이 뻗어나가는 수열에 규칙이 있지 않을까?"라는 생각이 들었다.
② 아이디어 열기
규칙 찾는 과정에서 예시를 들어 과정을 자세히 들여다보는 것만큼 중요한건 없는 것 같다..!!
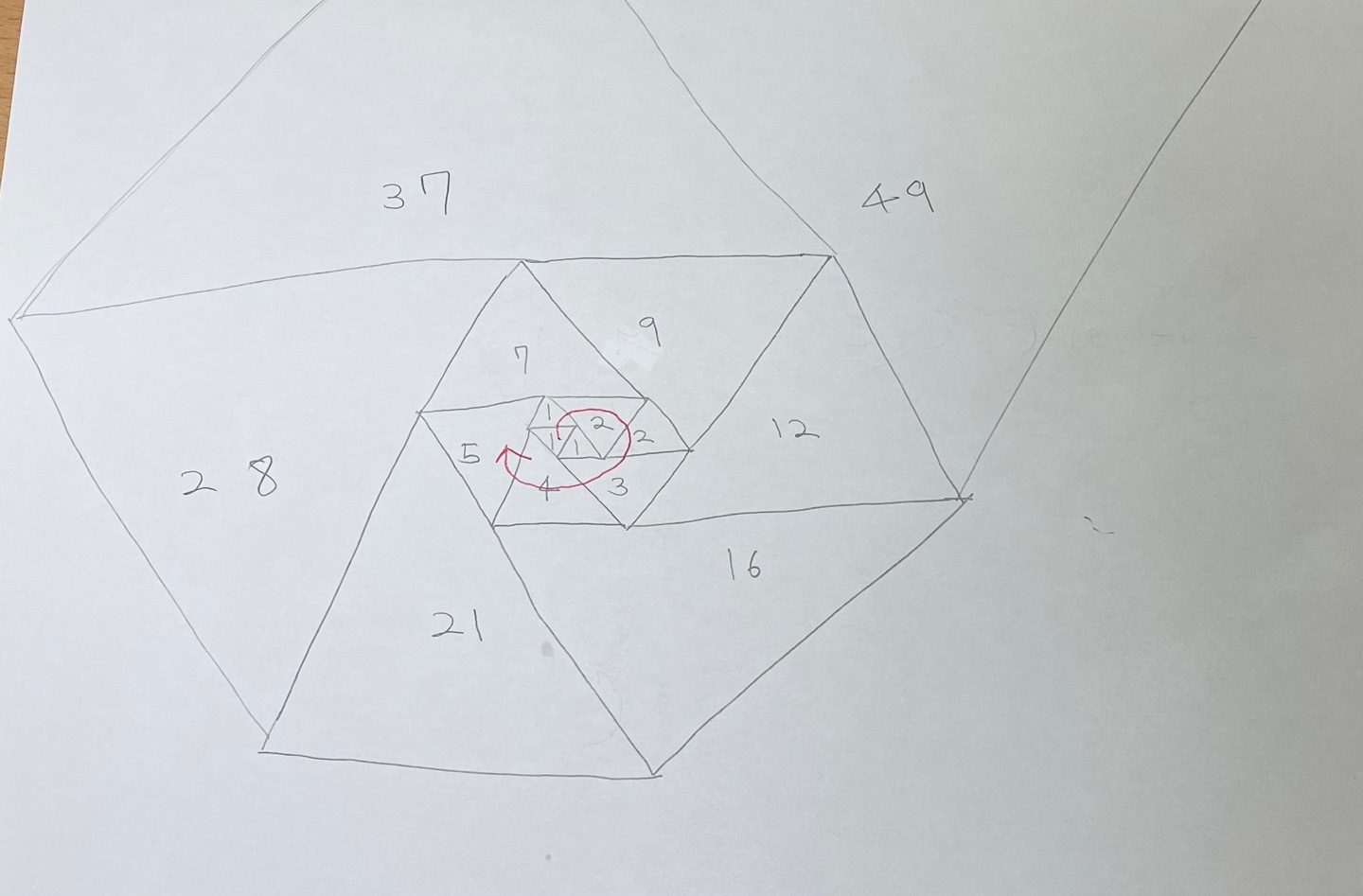
위 그림은 내가 직접 파도반 수열 모양을 그린 것이다.(그저 파도반 수열값을 구하기 위해 막 그린 거니 그림 퀄리티는 보장 못한다...!)
● 파도반 수열의 수는 다음과 같다.
1 1 1 2 2 3 4 5 7 9 12 16 21 28 37 49 ....
- 그림을 그리며 깨달을 건데 새로운 수열값이 만들어지기 위해서는 특정 두 수를 더하는데 그중 하나가 무조건적으로 바로 직전 수열값임을 깨달았다.
- 나머지 한 수는 무엇일까..??? 예를 들어 16의 경우를 보자. 16 = 12 + 4이다. 4라는 숫자는 16으로부터 5번째 이전의 수열값이다. 그렇다면 21의 경우를 보자. 21 = 16 + 5로 5 또한 마찬가지로 21으로부터 5번째 이전의 수열값이다.
그렇기에 점화식을 작성해본다면...
dp[i] = dp[i-1] + dp[i-5] (단, i>=6)
이를 코드로 구현하면 다음과 같다.
# 9461 파도반 수열
T = int(input())
for i in range(T) :
n = int(input())
if n == 1 : # n=1~5의 경우 그냥 출력
print(1)
elif n == 2 :
print(1)
elif n == 3 :
print(1)
elif n == 4 :
print(2)
elif n == 5 :
print(2)
else : # n이 6이상인 경우 dp점화식이용
dp = [0]*(n+1)
dp[1] = 1
dp[2] = 1
dp[3] = 1
dp[4] = 2
dp[5] = 2
for j in range(6,n+1) :
dp[j] = dp[j-1] + dp[j-5]
print(dp[n])후기
DP문제 특성상 과정을 들여다보며 규칙을 찾을려고 노력했던 것 같다..!!!
'Algorithm > dynamic programming' 카테고리의 다른 글
| [백준] 2133 타일 채우기 (파이썬 Python) (0) | 2021.07.25 |
|---|---|
| [백준] 1912 연속합 (파이썬 Python) (0) | 2021.07.25 |
| [백준] 11053 가장 긴 증가하는 부분 수열(LIS) (파이썬 Python) (0) | 2021.07.23 |
| [백준] 11057 오르막 수 (파이썬 Python) (0) | 2021.07.23 |
| [백준] 1932 정수 삼각형 (파이썬 Python) (0) | 2021.07.18 |