https://www.acmicpc.net/problem/11053
11053번: 가장 긴 증가하는 부분 수열
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이
www.acmicpc.net
문제 설명
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오.
예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이고, 길이는 4이다.
풀이 과정
- 나의 풀이
① 처음 이 문제를 풀었을 때 dp문제라는 감도 전혀 안 왔고 문제 해결을 위한 발상이 무척 힘들어 결국 못 풀었다. 구글링 중 이번 문제는 LIS문제로 dp문제 중 정말 유명한 문제임을 깨닫고 이 문제의 발상 및 해결과정에 대해 자세히 이해하고자 한다.
② 어째서 DP문제인가?
사실상 왜 DP문제인지... 이 문제가 DP문제유형임을 깨닫는 것 자체가 너무 힘들었다.
그래서 이번엔 정답코드를 보고 이를 직접 해석해봐야겠다.
# 11053
n = int(input())
array = list(map(int,input().split()))
dp = [1]*n
for i in range(n) :
for j in range(i) :
if array[i] > array[j] :
dp[i] = max(dp[i],dp[j]+1)
print(max(dp))이중 for문이 바로 DP문제의 해결과정인듯하다.
이해를 위해 예시를 들어보자.
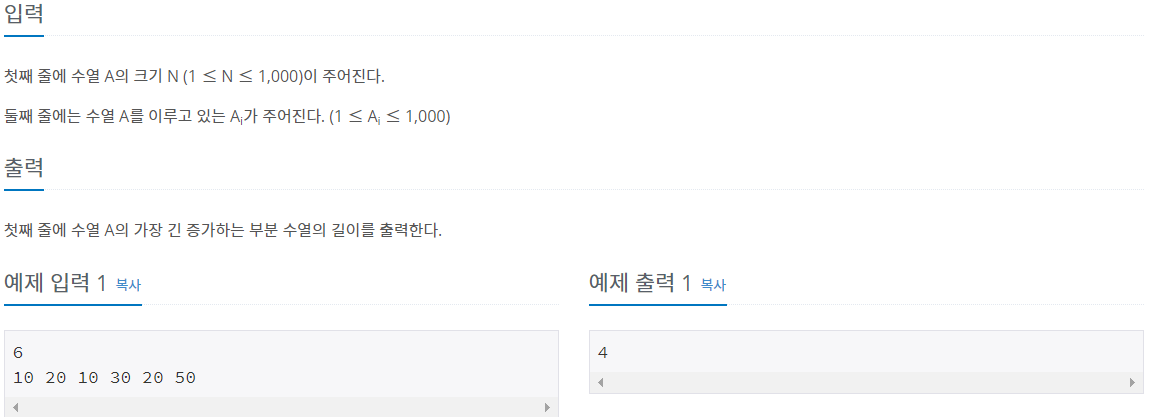
(1) '예제 입력 1' 의 경우와 같이 입력되었을 때 n=4, array=[10,20,10,30,20,50]이다.
(2) dp 테이블을 만든 이유는 아직까지 모르겠다.//#3번 문장까지의 해석
(3) 이중 for문 구조에서 i=4의 경우를 한번 살펴보자.
i=4,j=0; array[4](20) > array[0](10) : dp[4] = max(dp[4],dp[0]+1) = max(1,2) = 2
i=4,j=1; array[4](20) > array[1](20) : false
i=4,j=2; array[4](20) > array[2](10) : dp[4] = max(dp[4],dp[2]+1) = max(2,3) = 3
i=4,j=3; array[4](20) > array[3](30) : false
i=4,j=4; array[4](20) > array[4](20) : false
○ i=4 의 결과 : dp[4] = 3
(4) 이해하기
i=4인 경우.. 만약 array의 인덱스 4번째 항목의 수가 array의 인덱스 2번째 수보다 크다면 dp[4]는 dp[4]와 dp[2]+1 사이의 큰 수의 값이 된다.
왜냐하면 i=4인 경우를 계산할 당시 i=0,i=1,i=2,i=3 (즉,dp[0],dp[1],dp[2],dp[3])의 값이 전부 정해져있는 상황이다. 따라서 인덱스 4번째 항목의 수가 인데스 2번째 수보다 크면 dp[4]값은 최소한 dp[2]+1의 값은 확보한 것이다..!!!
하지만 그전에 dp[0]값 혹은 dp[1]값이 혹여나 d[2]+1값보다 클 수도 있기에 max함수를 사용하여 비교하여 dp[4]의 값을 갱신해주는 것이다.
그렇다... DP문제답게 중복되는 부분이 있고, 그에 따른 정보 갱신이 일어남을 알 수 있다. 드디어 왜 이 문제가 DP문제유형인지 깨달았다..!!
후기
역시 새로운 유형을 처음 배울 때는 정말 힘들다. 이제 익히는 과정이 필요하다. 이 문제유형의 문제들을 풀며 익혀보자.
'Algorithm > dynamic programming' 카테고리의 다른 글
| [백준] 1912 연속합 (파이썬 Python) (0) | 2021.07.25 |
|---|---|
| [백준] 9461 파도반 수열 (파이썬 Python) (0) | 2021.07.23 |
| [백준] 11057 오르막 수 (파이썬 Python) (0) | 2021.07.23 |
| [백준] 1932 정수 삼각형 (파이썬 Python) (0) | 2021.07.18 |
| [백준] 9095 1,2,3 더하기 (파이썬 Python) (0) | 2021.07.16 |