https://www.acmicpc.net/problem/2133
2133번: 타일 채우기
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.
www.acmicpc.net
문제 설명
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.
풀이 과정
- 나의 풀이
① 앞서 푼 2xn 타일링 1,2 문제와 같이 '타일링 문제는 점화식을 찾는 문제니깐 과정에서 규칙을 찾고 점화식으로 이어야겠구나'라는 생각을 하였다.
② 아이디어 열기
(1) n이 홀수인 경우 경우의 수가 없기에 0을 출력하도록 처리하였다.
(2) n이 짝수인 경우
n = 2 ; 3
n = 4 ; 11
n = 6 ; 41
....
n 값이 커질수록 경우의 수가 무척이나 불어나는 것을 확인하였다. 그리하여 결과를 통해 비교하는 것이 아닌 과정을 통한 점화식 작성이 필요함을 깨달았다.

위의 그림은 내가 규칙을 찾기 위해 적은 과정들이다.
(1) n=2일 때
직접 세어보니 3가지였다.
(2) n=4일 때
n=2일 때의 경우가 2번 겹친 모양이므로 3x3을 해주고, 새로운 모양이 추가되므로 +2를 해준다. 그러므로 3x3+2=11
(3) n=6일 때
n=2일 때의 경우가 3번 겹친 모양이므로 3x3x3을 해주고, 새로운 모양에 n=2일 때의 경우가 겹친 모양이 2번 있으므로 (2x3)x2를 해준다. 그러므로 3x3x3+(2x3)x2 = 41
이제 점화식을 세워 일반화과정을 거치자.
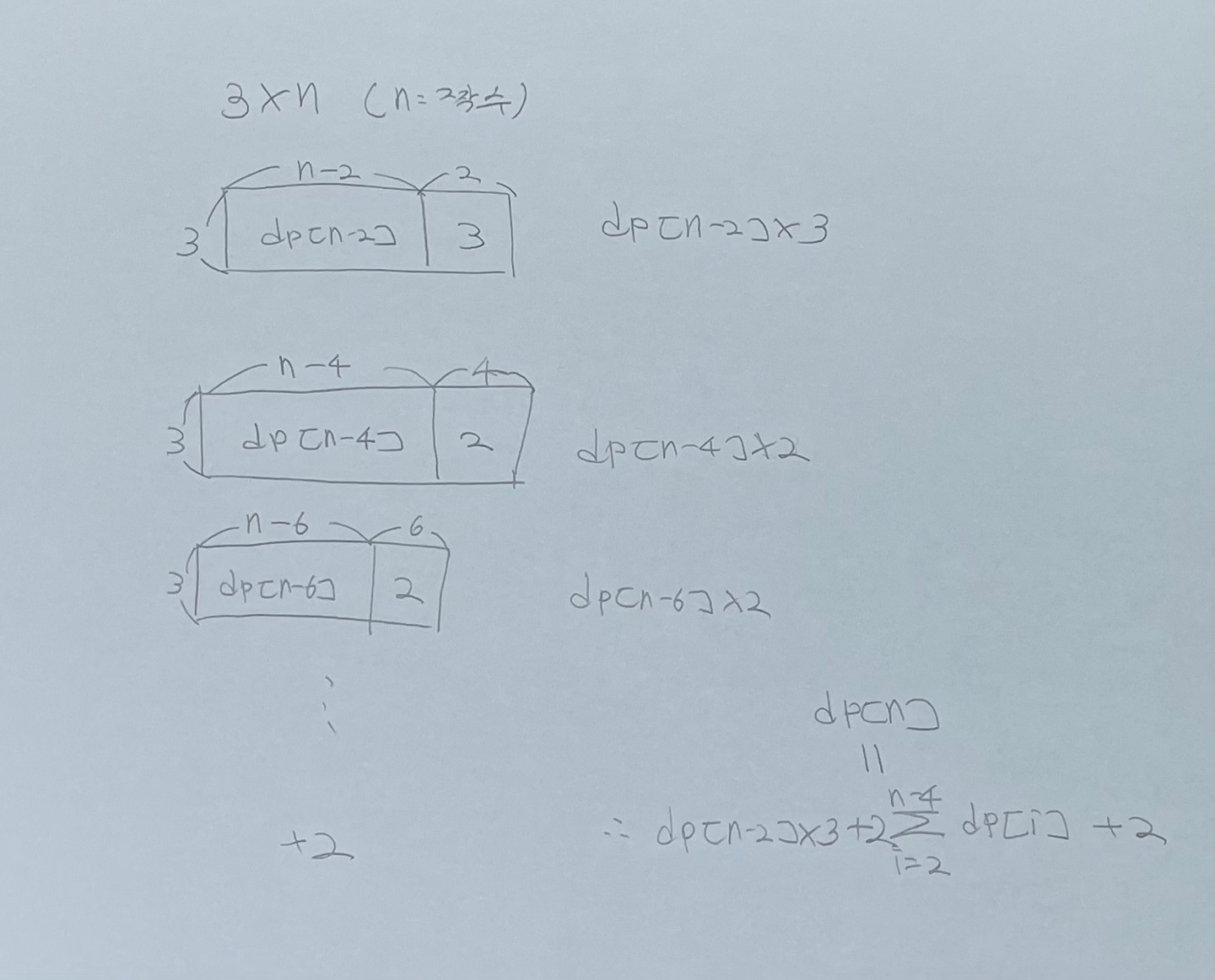
위의 그림에서 보듯이 n개의 타일을 고려해 일반화과정을 거쳤다. 사실상 첫번째 그림에서 찾을려고 했던 규칙과는 많이 다른 모습이다. (나도 이 부분에서 굉장히 시간을 많이 썼다.)
(1) n이 2씩 커질 때마다 새로운 모양이 2개씩 무조건 추가된다. (그러므로 마지막에 2를 더해준다.)
(2) 3x(n-2)개의 타일링에서 3x2개의 타일링을 추가하는 것이므로 dp[n-2]x3을 더 해준다.
(3) 이제 이 부분이 키포인튼데.. dp[n-2]는 분명 dp[n-2]를 구하는 과정에서 새로운 모양을 다 고려했겠지만 dp[n]을 구하는 과정에서 3x(n-4) + 4, 3x(n-6) + 6을 하면서 생기는 새로운 모양은 고려해주지 못했기에 시그마를 통해 합을 구해준다.
말로 설명하기 굉장히 힘든 부분인데.. 최대한 말로 설명해보겠다.
분명 n=4,n=6,n=8을 추가할 때마다 새로운 모양이 2개씩 추가된다. 새로운 모양을 추가하며 고려되는 모양은 전부 2를 곱해주는 과정을 통해 더해준다.
dp[n]을 구하는 과정에서 dp[n-2]는 3x(n-4) + 4, 3x(n-6) + 6을 하면서 생기는 새로운 모양은 고려해주지 못했기에...!!! 더해주어야한다는 것이다.
이를 점화식의 형태로 표현하면 다음과 같다.
dp[n] = 3*dp[n-2] + 2*(dp[n-4]+dp[n-6]+....dp[2]) + 2
이를 코드로 구현하면 다음과 같다.
# 2133 타일 채우기
n = int(input())
if n == 1 :
print(0)
else :
dp = [0]*(n+1)
dp[2] = 3
for i in range(4,n+1) :
if i%2 == 1 :
dp[i] = 0
else :
dp[i] = dp[i-2]*3 + sum(dp[:i-2])*2 + 2
print(dp[n])후기
타일링은 역시 점화식 찾기 싸움이지만 이문제는 너무 어려웠다 ....ㅠㅠ...
'Algorithm > dynamic programming' 카테고리의 다른 글
| [백준] 2156 포도주 시식 (파이썬 Python) (0) | 2021.07.26 |
|---|---|
| [백준] 2578 계단 오르기 (파이썬 Python) (0) | 2021.07.26 |
| [백준] 1912 연속합 (파이썬 Python) (0) | 2021.07.25 |
| [백준] 9461 파도반 수열 (파이썬 Python) (0) | 2021.07.23 |
| [백준] 11053 가장 긴 증가하는 부분 수열(LIS) (파이썬 Python) (0) | 2021.07.23 |