https://www.acmicpc.net/problem/1912
1912번: 연속합
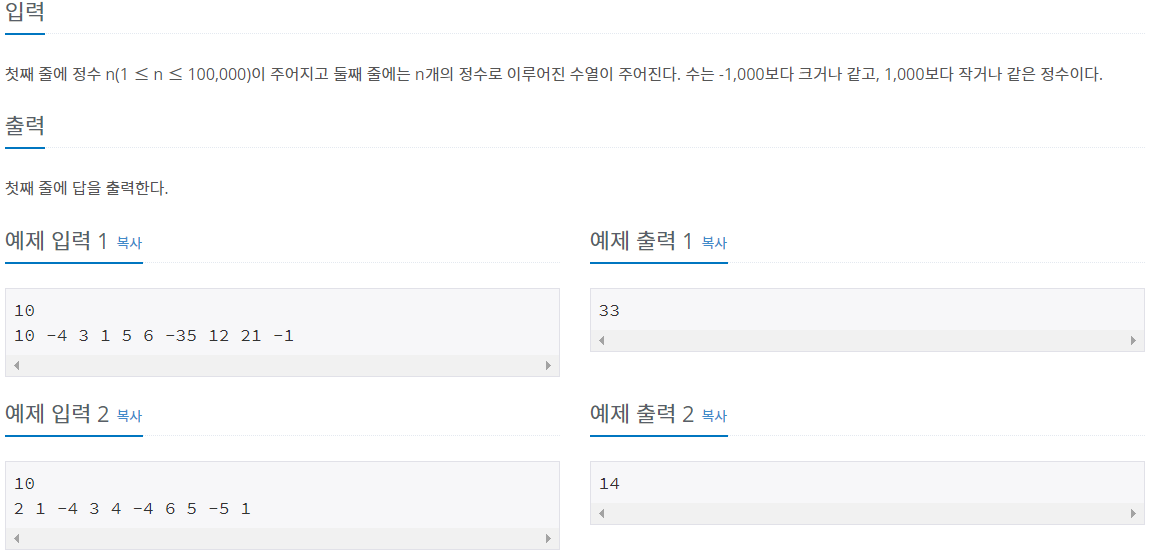
첫째 줄에 정수 n(1 ≤ n ≤ 100,000)이 주어지고 둘째 줄에는 n개의 정수로 이루어진 수열이 주어진다. 수는 -1,000보다 크거나 같고, 1,000보다 작거나 같은 정수이다.
www.acmicpc.net
문제 설명
n개의 정수로 이루어진 임의의 수열이 주어진다. 우리는 이 중 연속된 몇 개의 수를 선택해서 구할 수 있는 합 중 가장 큰 합을 구하려고 한다. 단, 수는 한 개 이상 선택해야 한다.
예를 들어서 10, -4, 3, 1, 5, 6, -35, 12, 21, -1 이라는 수열이 주어졌다고 하자. 여기서 정답은 12+21인 33이 정답이 된다.
풀이 과정
- 나의 풀이
① "주어진 배열에 있어서 최선의 선택을 해야하니깐... max함수를 이용한 DP문제가 아닐까?" 라는 생각이 먼저 들었다.
② 일단... 너무 많은 경우의 수가 있다. n=10만 되더라도 55개의 경우의 수가 존재한다. 그 모든 경우의 수를 리스트에 집어넣고 max함수를 쓰기에는 시간복잡도가 비약적으로 상승할 거 같아... 경우의 수를 최대한 줄여 최선의 경우에 대해서만 생각하는 방향으로 DP식을 짜야겠다고 생각하였다.
③ 아이디어 열기
(1) 상향식을 이용하여 배열의 숫자를 순차적으로 걸러내며 최댓값을 계속 갱신한 뒤 마지막에 최댓값을 출력하기로 계획하였다.
(2) 이 문제의 포인트이자 어려운 부분이 바로 배열의 숫자를 순차적으로 걸러내는 동적계획과정인듯하다...
(3) 예제 1 번을 살펴보자. 첫번째 항목인 10부터 여섯 번째 항목인 6까지의 합이 세번째 항목 3부터 여섯 번째 항목 6까지의 합보다 큼을 알 수 있다.
또한 8번째항목 12부터 9번째항목 21까지의 합이 7번째 항목 -35부터 9번째항목 21까지의 합보다 큼을 알 수 있다.
(4) dp의 항목을 n의 값만큼 늘리고, 상향식을 이용하여 점화식을 작성하면 다음과 같다.
(5)
dp[i] = max(dp[i-1]+array[i],array[i])
예를 들어 1 5 6 -35 12 21 의 경우 dp=[1,6,12,-23,12,33]으로 5번째 항목에서 새로운 값으로 갱신됨을 알 수 있다. 간략히 말하자면 항목의 값을 계속해서 더해나가는 과정에서 다음 항목의 값을 더한 경우가 그당시의 최댓값보다 작다면 그당시의 최댓값까지 끊고 새로운 최댓값을 찾는다!
(6) 이를 코드로 구현하면 다음과 같다.
# 1912 연속합
n = int(input())
array = list(map(int,input().split()))
dp = [0]*n
result = -1001
for i in range(0,n) :
dp[i] = max(dp[i-1]+array[i],array[i])
result = max(dp[i],result)
print(result)후기
LIS 문제유형이랑 매우 흡사하다고 느꼈지만 배열의 숫자를 순차적으로 거름에 있어서 정말 어려웠던 문제였던 것 같다.
'Algorithm > dynamic programming' 카테고리의 다른 글
| [백준] 2578 계단 오르기 (파이썬 Python) (0) | 2021.07.26 |
|---|---|
| [백준] 2133 타일 채우기 (파이썬 Python) (0) | 2021.07.25 |
| [백준] 9461 파도반 수열 (파이썬 Python) (0) | 2021.07.23 |
| [백준] 11053 가장 긴 증가하는 부분 수열(LIS) (파이썬 Python) (0) | 2021.07.23 |
| [백준] 11057 오르막 수 (파이썬 Python) (0) | 2021.07.23 |