https://www.acmicpc.net/problem/9251
9251번: LCS
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다. 예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.
www.acmicpc.net
문제 설명
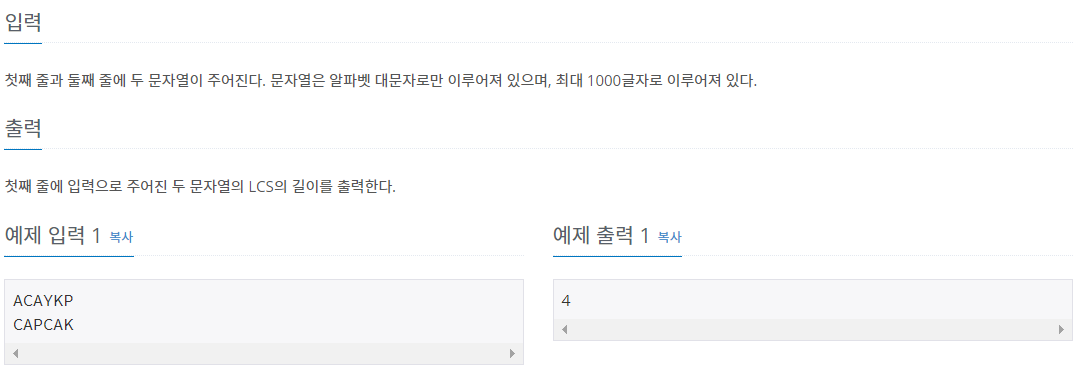
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.
예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.
문제 풀이
- 나의 풀이
① 이 문제에서 직관적으로 파악한 것은 'LIS와 비슷한 유형인 것 같고.. DP문제겠구나..!!'였다.
② 아이디어 열기
어떻게 DP를 저장할지에 대해 생각해보던 중... 이중 for문을 이용해 첫번째 입력값과 두번째 입력값을 비교하며 풀기로 했다.
DP에 저장하는 방식은 2차원 리스트 배열형태를 이용하였다.
# 9251 LCS
S1 = list(input())
S2 = list(input())
len1 = len(S1)
len2 = len(S2)
dp = [[0]*(len2 + 1) for _ in range(len1+1)]
print(dp)
for i in range(1,len1 + 1) :
for j in range(1,len2 + 1) :
if S1[i-1] == S2[j-1] :
dp[i][j] = dp[i-1][j-1] + 1
else :
dp[i][j] = max(dp[i-1][j],dp[i][j-1])
print(dp)
print(dp[len1][len2])이해를 돕기 위해 표를 준비했다..!!
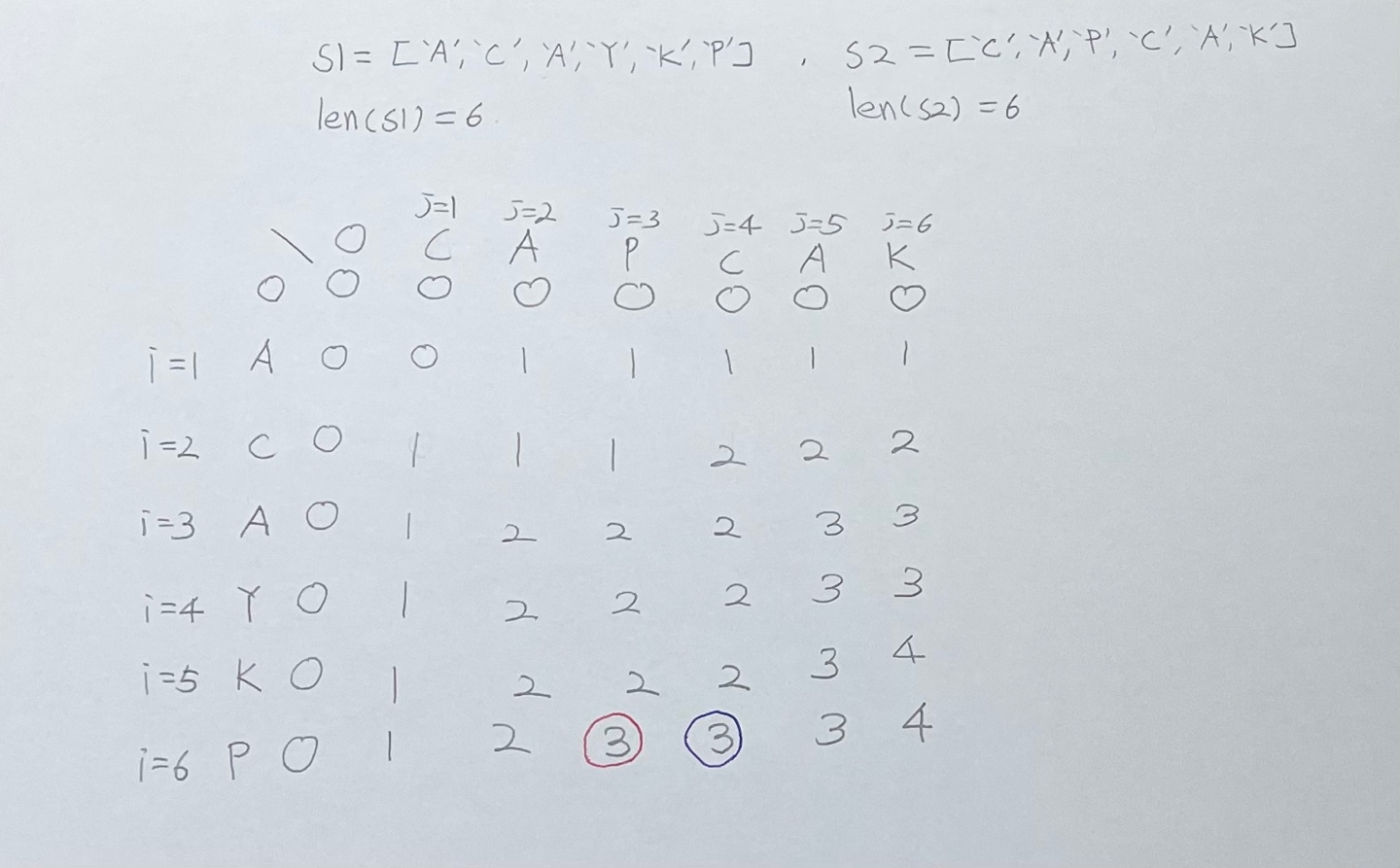
조건은 i는 고정된 채로 j를 늘려가며 비교하는 경우 같은 숫자가 나오면 무조건 +1을 하고 아니라면 dp[i-1][j]와 dp[i][j-1] 중 큰 수로 정하기로 하자.
우리가 출력하는 값은 마지막 dp[len1][len2]로서 마지막 수이다.
○ 위 표에서 빨간색 동그라미가 그려진 숫자 3을 보자.
알파벳 P가 나왓으니 자연스럽게 +1을 해준다.
○ 위 표에서 파란색 동그라미가 그려진 숫자 3을 보자.
dp[6][3] = 3 (이건 CAP가 LCS)
dp[5][4] = 2 (이건 CA가 LCS)
i=6 입장에서는 3이 더 크니 3을 채택한다.
번외로 이 문제 풀면서 dp테이블을 작성하는데 큰 어려움이 있었다.. 아래 접은 글을 통해 참고만 하시길..
파이스크립터를 사용하는 나는 출력되는 값을 신뢰하는 편이다.
문제풀이 과정에서 다음과 같은 이차원 배열 리스트를 만들어야하는데..
[[0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0]]
내가 처음 정한 dp테이블은 dp = [[0]*(len2+1)]*(len1+1) 이었다. 이것이 의미하는 것은
[[0,0,0,0,0,0,0,0,0,0], [0,0,0,0,0,0,0,0,0,0], [0,0,0,0,0,0,0,0,0,0], [0,0,0,0,0,0,0,0,0,0], [0,0,0,0,0,0,0,0,0,0]] 이처럼 1차원 배열 리스트였다..!!
그제서야 for문을 이용한 이유가 맨 위와 같이 이차원 배열 리스트를 이용하기 위해서임을 깨달았다..!!
참고로 [[0 for _ in range(len2 + 1)] for _ in range(len1 + 1)] 은 옳은 경우이다. 왜냐하면 안쪽에 0을 일차원 배열 리스트형식으로 배열했기 때문이다..!!!
★ 이차원 배열리스트를 만들 때는 항상 다음과 같은 형식으로 만들기..!!
[[0]*n for _ in range(m)] <- 가로가 n, 세로가 m
후기
dp문제를 풀면 내가 똑똑하지 않음을 너무 잘 느껴버린다. ㅠ.. ㅋㅋ
'Algorithm > dynamic programming' 카테고리의 다른 글
| [백준] 10164 격자상의 경로 (파이썬 Python) (0) | 2021.08.07 |
|---|---|
| [백준] 9465 스티커 (파이썬 Python) (0) | 2021.08.01 |
| [백준] 1309 동물원 (파이썬 Python) (0) | 2021.07.30 |
| [백준] 2780 비밀번호 (파이썬 Python) (0) | 2021.07.30 |
| [백준] 2156 포도주 시식 (파이썬 Python) (0) | 2021.07.26 |