https://www.acmicpc.net/problem/10164
10164번: 격자상의 경로
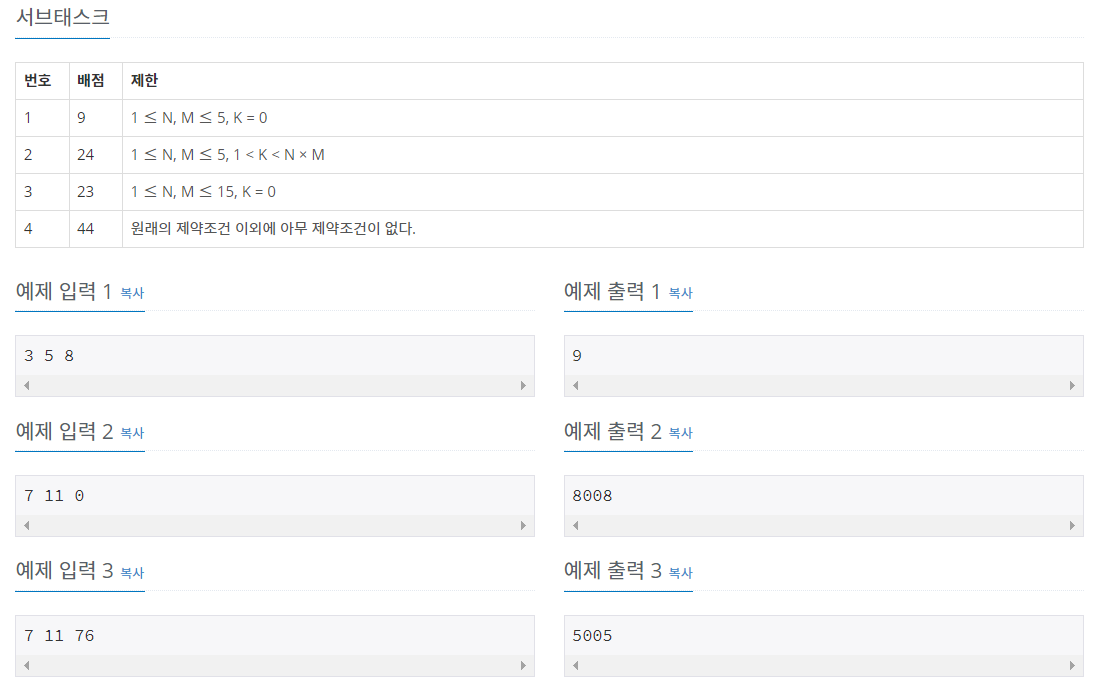
입력의 첫째 줄에는 격자의 행의 수와 열의 수를 나타내는 두 정수 N과 M(1 ≤ N, M ≤ 15), 그리고 ○로 표시된 칸의 번호를 나타내는 정수 K(K=0 또는 1 < K < N×M)가 차례로 주어지며, 각 값은 공백으
www.acmicpc.net
문제 설명
행의 수가 N이고 열의 수가 M인 격자의 각 칸에 1부터 N×M까지의 번호가 첫 행부터 시작하여 차례로 부여되어 있다. 격자의 어떤 칸은 ○ 표시가 되어 있다. (단, 1번 칸과 N × M번 칸은 ○ 표시가 되어 있지 않다. 또한, ○ 표시가 되어 있는 칸은 최대 한 개이다. 즉, ○ 표시가 된 칸이 없을 수도 있다.)
행의 수가 3이고 열의 수가 5인 격자에서 각 칸에 번호가 1부터 차례대로 부여된 예가 아래에 있다. 이 격자에서는 8번 칸에 ○ 표시가 되어 있다.

풀이 과정
- 나의 풀이 1 (수학적으로 접근)
① 아이디어 열기
고등학교 확통 과정에서 배운 최단경로 경우의 수 문제유형과 매우 유사함을 느꼈다.
k가 0일 때는 그저 (n+m)!//(n!*m!)을 해주면 된다.
k가 0이 아닐 때는 k의 위치와 최종 위치를 좌표화시킨 후 계산해주면 되겠다고 생각했다.
내가 느끼기에 이 풀이의 키포인트는 k의 위치와 최종 위치의 좌표화이다. 둘 다 (n,m)의 형태로 좌표화하자.
● k의 위치 (dotN1,dotM1)
dotN1 = (k-1)//m + 1
(k-1)을 하고 m으로 나눈 몫은 몇번째 줄부터 0,1,2,3... 순으로 이어지므로 마지막에 +1을 해준다.
dotM1 = k - (dotN1-1)*m
dotN1을 구한 상황에서 생각해보자. m값은 끝의 수가 5,10,15로 m의 배수이다. 따라서 dotM1값은 dotM1이 같은 가로줄의 수 중에서 몇번째 수인지를 나타내는 것이기에 k값에 (dotN1-1)*m값을 빼준다.
● 최종 위치 (dotN2,dotM2) (계산을 위해서 k의 위치를 1,1으로 잡은 경우로 계산해주자.)
dotN2 = n - (dotN1-1)
dotM2 = m - (dotM1-1)
② 코드 구현
import sys
import math
input = sys.stdin.readline
n,m,k = map(int,input().split())
dotN1 = (k-1)//m + 1
dotM1 = k - (dotN1-1)*m
dotN2 = n - (dotN1-1)
dotM2 = m - (dotM1-1)
if k == 0 :
print((math.factorial(n+m-2)//(math.factorial(n-1)*math.factorial(m-1))))
else :
first = (math.factorial(dotN1+dotM1-2)//(math.factorial(dotN1-1)*math.factorial(dotM1-1)))
second = (math.factorial(dotN2+dotM2-2)//(math.factorial(dotN2-1)*math.factorial(dotM2-1)))
print(first*second)결과는..!!

성공!!
- 나의 풀이 2 (dp로 풀기)
① 아이디어 열기
이번에는 dp로 풀어볼 것이다. 생각해보니 고등학교 확통 과정에서 배운 최단경로 경우의 수 문제유형을 풀 때 첫번째 풀이와 같이 공식을 사용하지 않고 직접 숫자를 메겨가며 구하기도 했었기에 그 방법을 dp를 이용하여 사용해볼려고 한다.
② 코드 구현
import sys
input = sys.stdin.readline
n,m,k = map(int,input().split())
def find(n,m) :
dp = [[0]*(m+1)]*(n+1)
for i in range(1,n+1) :
for j in range(1,m+1) :
if i == 1 and j == 1 :
dp[i][j] = 1
continue
dp[i][j] = dp[i-1][j] + dp[i][j-1]
return dp[n][m]
if k == 0 :
print(find(n,m))
else :
dotN1 = (k-1)//m + 1
dotM1 = k - (dotN1-1)*m
dotN2 = n - (dotN1-1)
dotM2 = m - (dotM1-1)
first = find(dotN1,dotM1)
second = find(dotN2,dotM2)
print(first*second)
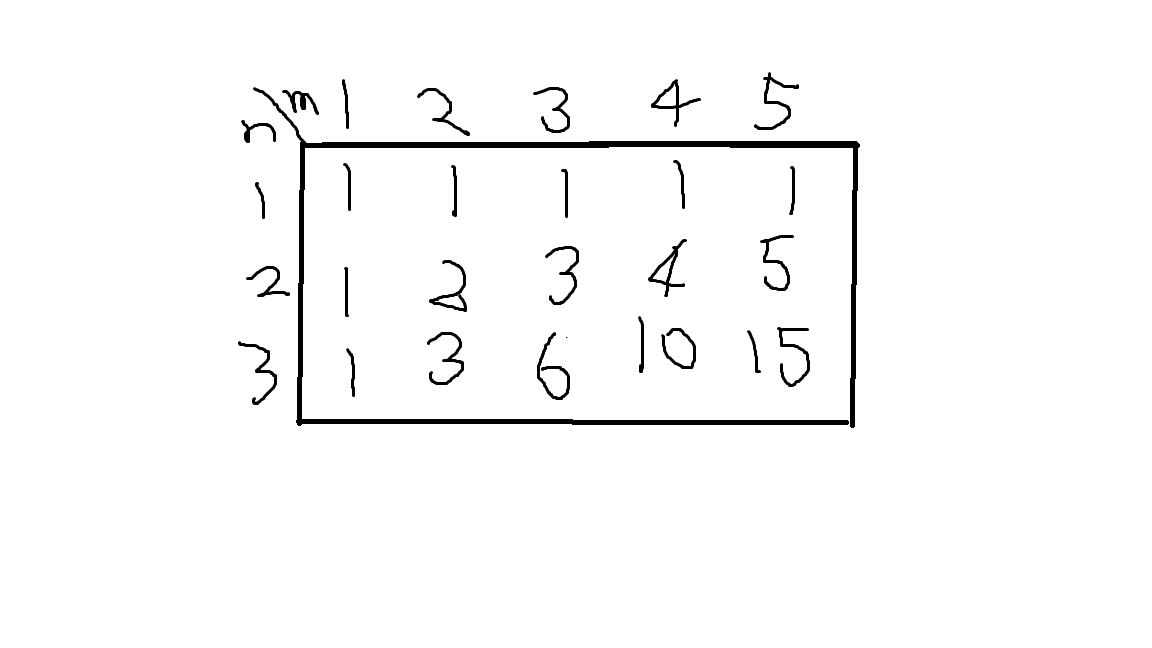
dp 테이블에 위의 그림과 같은 방식으로 저장해주었다.
결과는...!

성공..!!
후기
확통 배울 때가 기억났던 문제..!!
'Algorithm > dynamic programming' 카테고리의 다른 글
| [백준] 9251 LCS (파이썬 Python) (0) | 2021.08.08 |
|---|---|
| [백준] 9465 스티커 (파이썬 Python) (0) | 2021.08.01 |
| [백준] 1309 동물원 (파이썬 Python) (0) | 2021.07.30 |
| [백준] 2780 비밀번호 (파이썬 Python) (0) | 2021.07.30 |
| [백준] 2156 포도주 시식 (파이썬 Python) (0) | 2021.07.26 |