https://www.acmicpc.net/problem/1934
1934번: 최소공배수
두 자연수 A와 B에 대해서, A의 배수이면서 B의 배수인 자연수를 A와 B의 공배수라고 한다. 이런 공배수 중에서 가장 작은 수를 최소공배수라고 한다. 예를 들어, 6과 15의 공배수는 30, 60, 90등이 있
www.acmicpc.net
문제 설명
두 자연수 A와 B에 대해서, A의 배수이면서 B의 배수인 자연수를 A와 B의 공배수라고 한다. 이런 공배수 중에서 가장 작은 수를 최소공배수라고 한다. 예를 들어, 6과 15의 공배수는 30, 60, 90등이 있으며, 최소 공배수는 30이다.
두 자연수 A와 B가 주어졌을 때, A와 B의 최소공배수를 구하는 프로그램을 작성하시오.
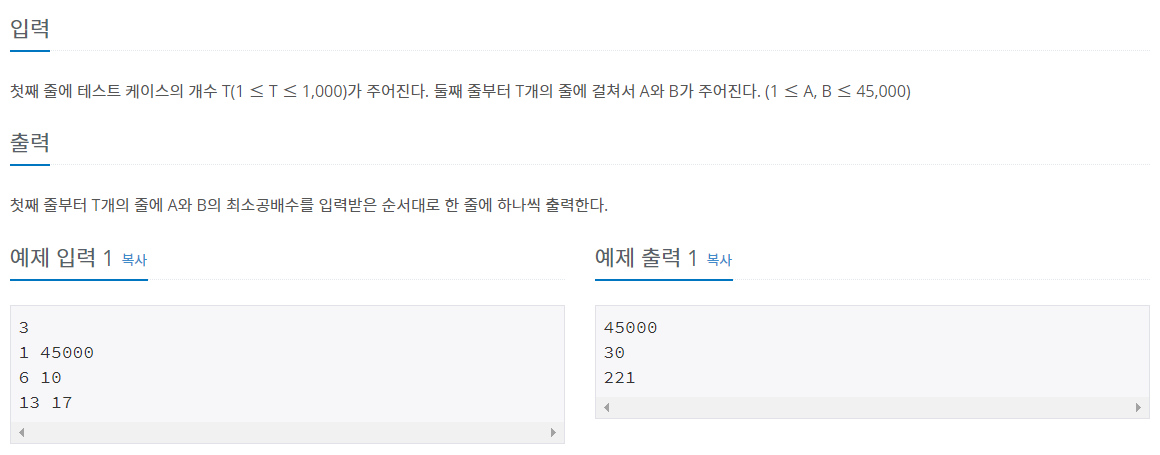
풀이 과정
- 나의 풀이
① 최대공약수 구하는 법
유클리드 호제법을 통해 최대공약수를 쉽게 구할 수 있다.
유클리드 호제법이란 기원전 300년 전에 나온 가장 오래된 알고리즘으로 유명하다.
유클리드 호제법으로 최대공약수를 구하는 방법은 다음과 같다.
○ 두 자연수 a,b에 대하여 a를 b로 나눈 나머지 r에 대해 a와 b의 최대공약수는 b와 r의 최대공약수와 같다. 이를 계속 반복하며 b가 0이 될 때, a값이 바로 최대공약수이다. (재귀와 반복이 느껴진다..!!)
② 최소공배수 구하는 법
입력값인 두 정수 a,b에 대하여 a = x * gcd , b = y * gcd (단, gcd는 a와 b의 최대공약수이고, x와 y는 서로 서로소 관계이다.) 이므로 최소공배수는 a*b//gcd가 된다..!!
이를 코드로 구현하면 다음과 같다.
import sys
input = sys.stdin.readline
T = int(input())
def gcd_r(a,b) :
if b == 0 :
return a
else :
return gcd_r(b,a%b)
def gcd_for(a,b) :
while b > 0 :
tmp = a % b
a = b
b = tmp
return a
def lcm(a,b) :
return a*b//gcd_for(a,b)
for _ in range(T) :
a,b = map(int,input().split())
print(lcm(a,b))○ gcd_for 함수는 반복문을 이용하였고, gcd_r 함수는 재귀를 이용하였다.
'Algorithm > math' 카테고리의 다른 글
| [백준] 9613 GCD 합 (파이썬 Python) (0) | 2021.08.13 |
|---|---|
| [백준] 13241 최소공배수 (파이썬 Python) (0) | 2021.08.13 |
| [백준] 2702 초6 수학 (파이썬 Python) (0) | 2021.08.13 |
| [백준] 1193 분수 찾기 (파이썬 Python) (0) | 2021.08.11 |
| [백준] 1011 Fly me to the Alpha Centauri (파이썬 Python) (0) | 2021.07.08 |